Ми часто дивимось на м’яч, планету чи навіть краплю води — і не задумуємось, що всі вони мають одну спільну геометричну красу: форму сфери. Але коли потрібно порахувати, скільки поверхні має така форма, більшість губиться. Насправді, площа сфери — це не складно. Варто лише зрозуміти логіку за простою формулою, і вона запам’ятається надовго.
Що таке сфера простими словами
Сфера — це поверхня, утворена всіма точками, які знаходяться на однаковій відстані від центру. Якщо взяти звичайний тенісний м’яч, його поверхня — це і є сфера, а сама «всередині» — куля. Коли ми говоримо про площу сфери, маємо на увазі площу саме цієї зовнішньої оболонки.
Уявіть, що ви хочете обгорнути кулю плівкою або пофарбувати її. Кількість матеріалу, яка піде на покриття, — це і є площа поверхні. Від цього прикладу легше зрозуміти, чому така тема важлива не лише у математиці, а й у звичайному житті.
«Математика стає простою, коли її можна побачити очима.»
Формула площі сфери
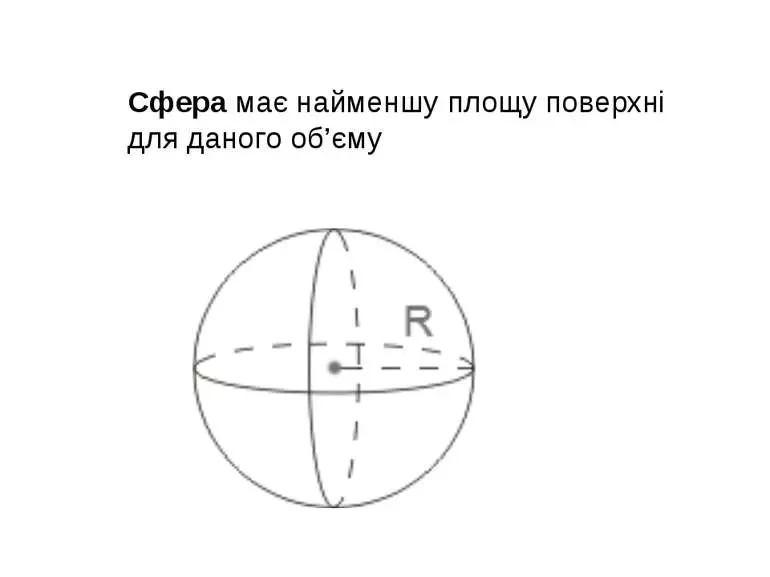Основна формула виглядає коротко і зрозуміло:
S = 4πr²,
де S — площа, r — радіус, а π — відоме число «пі», приблизно 3,14.
Щоб знайти площу сфери, треба знати лише радіус. Наприклад, якщо радіус кулі дорівнює 5 см, підставляємо у формулу:
S = 4 × 3,14 × 25 = 314 см².
А якщо у вас є діаметр (d), а не радіус, можна скористатись формулою S = πd². Це той самий принцип, тільки через іншу змінну.
Тут важливо не просто запам’ятати, а відчути логіку. Площа поверхні зростає пропорційно квадрату радіуса. Тобто якщо збільшити радіус удвічі — площа збільшиться в чотири рази. Це легко перевірити на прикладах.
Як запам’ятати формулу на практиці
Коли щось здається складним, допомагають побутові порівняння. Уявіть, що ви маєте невелику кулю і велику кулю для боулінгу. Якщо збільшити розмір лише вдвічі, то фарби для покриття потрібно не вдвічі більше, а в чотири рази! Саме тому 4πr² так точно описує залежність площі від розміру.
Спробуйте зробити простий експеримент:
Візьміть два повітряні кульки різного розміру.
Виміряйте їхні діаметри.
Порахуйте площу за формулою.
Так ви на власні очі побачите, як швидко зростає площа, коли збільшується радіус.
М’який заклик: спробуйте повторити це самі — лише тоді формула справді «приживеться» у пам’яті.
Звідки береться формула
Для тих, хто любить знати, «чому саме так», є цікаве пояснення. Якщо розрізати кулю на тонкі «шари» і розкласти їх у вигляді циліндра, то виявиться, що сумарна площа цих шарів дорівнює поверхні циліндра без кришок. Саме так Архімед колись довів, що площа сфери = 4πr².
У цьому є краса: складна тривимірна форма підкоряється простому правилу. І коли ви дивитесь на глобус чи апельсин, ви вже можете оцінити — скільки квадратних сантиметрів займає їхня поверхня.
«Найкращі відкриття народжуються зі звичайного запитання: чому так?»
Приклади з життя
Формула площі сфери потрібна не лише в задачах з підручника.
Будівництво та дизайн: архітектори рахують площу куполів.
Інженери: визначають поверхню сферичних резервуарів, щоб порахувати фарбу чи теплоізоляцію.
Астрономи: оцінюють площу поверхні планет, щоб розуміти, як розподіляється тепло від Сонця.
А якщо подивитись у побут — навіть при виготовленні шоколадних кульок чи ялинкових іграшок формула 4πr² виявляється корисною.
Наприкінці будь-яких розрахунків завжди запитуйте себе: «Який реальний розмір цього об’єкта?» — це допоможе не лише розуміти математику, а й мислити об’ємно.
Як знайти площу сфери за площею
Іноді задача ставиться навпаки — відома площа, треба знайти радіус.
Формулу можна просто «перевернути»:
r = √(S / 4π)
Приклад: якщо площа сфери дорівнює 314 см²,
r = √(314 / 12,56) ≈ 5 см.
Це той самий принцип, тільки в зворотному напрямку.
Спробуйте розв’язати кілька таких прикладів — це зміцнить розуміння формули.
Чим більше практики, тим менше страху перед абстрактними символами.
Математика стає зрозумілою, коли перестає бути набором сухих формул. Площа сфери — це не просто рівняння з π та r. Це спосіб побачити зв’язок між формою, простором і тим, як усе в природі взаємопов’язане.
Наступного разу, коли триматимете в руках м’яч або дивитиметесь на Місяць, пригадайте просту формулу 4πr². За нею — тисячоліття людського спостереження і краса точності.
М’який заклик: не обмежуйтесь підручниками — спробуйте рахувати те, що бачите навколо. І тоді математика стане частиною вашого щоденного мислення.
